The maximum subsequence sum algorithm

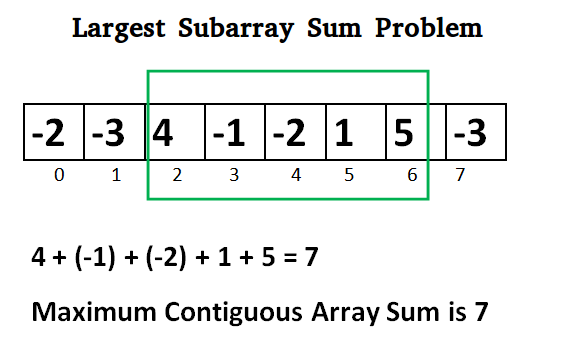
The maximum subsequence sum algorithm is a classic problem in computer science. The problem is to find the maximum sum of a contiguous subsequence in an array of integers. The algorithm has a number of different implementations with different time complexities. The following are some of the most common implementations of the algorithm.

Table of Contents

1. Cubic implementation
2. Quadratic implementation
3. Linearithmic implementation
4. Linear implementation

Cubic Algorithm \(O(n^3)\)

This implementation uses three nested loops to iterate over all possible subarrays of the input array and calculate the sum of each subarray. The maximum sum is then updated if a larger sum is found.

public static int maxSubSum1(int[] a) {
    int maxSum = 0;
    for (int i = 0; i < a.length; i++) {
        for (int j = i; j < a.length; j++) {
            int thisSum = 0;
            for (int k = i; k <= j; k++) {
                thisSum += a[k];
            }
            if (thisSum > maxSum) {
                maxSum = thisSum;
            }
        }
    }
    return maxSum;
}

Quadratic Algorithm \(O(n^2)\)

This implementation is an improvement over the cubic algorithm. It calculates the sum of each subarray according to the previous sum instead of recalculating the sum from scratch which makes the last nested loop unnecessary.

public static int maxSubSum2(int[] a) {
    int maxSum = 0;
    for (int i = 0; i < a.length; i++) {
        int thisSum = 0;
        for (int j = i; j < a.length; j++) {
            thisSum += a[j];
            if (thisSum > maxSum) {
                maxSum = thisSum;
            }
        }
    }
    return maxSum;
}

Linearithmic Algorithm \(O(nlogn)\)

This implementation uses a divide-and-conquer approach to solve the problem. It divides the input array into two halves and recursively calculates the maximum subsequence sum for each half. It then combines the results to find the maximum subsequence sum for the entire array.

public static int maxSubSum3(int[] a) {
    return maxSumRec(a, 0, a.length - 1);
} 
int maxSumRec(int[] a, int left, int right) {
    if (left == right) {
        if (a[left] > 0) {
            return a[left];
        } else {
            return 0;
        }
    }
    int center = (left + right) / 2;
    int maxLeftSum = maxSumRec(a, left, center);
    int maxRightSum = maxSumRec(a, center + 1, right);
    int maxLeftBorderSum = 0, leftBorderSum = 0;
    for (int i = center; i >= left; i--) {
        leftBorderSum += a[i];
        if (leftBorderSum > maxLeftBorderSum) {
            maxLeftBorderSum = leftBorderSum;
        }
    }
    int maxRightBorderSum = 0, rightBorderSum = 0;
    for (int i = center + 1; i <= right; i++) {
        rightBorderSum += a[i];
        if (rightBorderSum > maxRightBorderSum) {
            maxRightBorderSum = rightBorderSum;
        }
    }
    return max3(maxLeftSum, maxRightSum, maxLeftBorderSum + maxRightBorderSum);
}
int max3(int a, int b, int c) {
    return a > b ? (a > c ? a : c) : (b > c ? b : c);
}

Linear Algorithm \(O(n)\)

This implementation is the most efficient and uses a linear algorithm to solve the problem. It iterates over the input array once and calculates the maximum subsequence sum using a single loop.

public static int maxSubSum4(int[] a) {
    int maxSum = 0;
    int thisSum = 0;
    for (int i = 0; i < a.length; i++) {
        thisSum += a[i];
        if (thisSum > maxSum) {
            maxSum = thisSum;
        } else if (thisSum < 0) {
            thisSum = 0;
        }
    }
    return maxSum;
}

• 2025 2
• 2024 3
• 2023 1
• 2022 2