The Convex Hull Problem

The convex hull problem is a problem in computational geometry. It is about finding the smallest convex polygon that contains a given set of points. The convex hull problem has many applications in computer graphics, pattern recognition, and image processing. In this post, we will discuss some algorithms to solve the convex hull problem.

1. The brute force algorithm

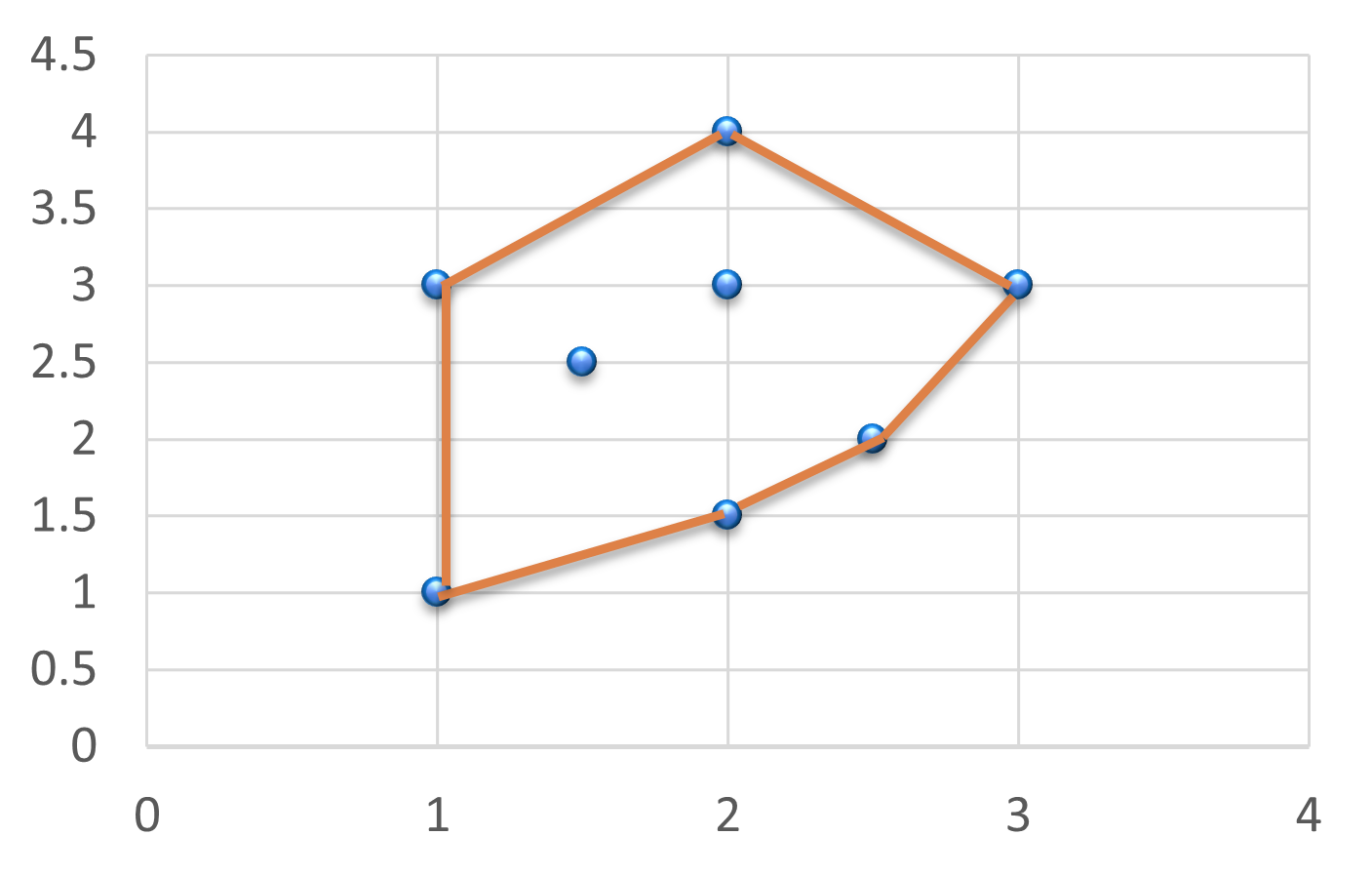
The brute force algorithm is the simplest algorithm to solve the convex hull problem. It works by checking all possible combinations of points to find the convex hull. The algorithm has a time complexity of O(n^3), where n is the number of points. The brute force algorithm is not practical for large datasets, but it is useful for small datasets to verify the correctness of other algorithms.

1.1 The general idea

for every pair of points (i, j) in the set of points
    if all other points are on the same semiplane defined by the line (i, j)
        add the line (i, j) to the convex hull
    end if
end for

1.2 Lets move to the implementation

The first step is to define the Point class. The Point class will have two attributes, x and y, to represent the coordinates of the point.

class Point{
    int x;
    int y;
    Point(int x, int y){
        this.x = x;
        this.y = y;
    }
    // Compute the distance between two points
    Double distance(Point p){
        return Math.sqrt( Math.pow(this.x - p.x,2) + Math.pow(this.y - p.y,2));
    }
    @Override
    public String toString() {
        return "<" + x + ", " + y + ">";
    }
}

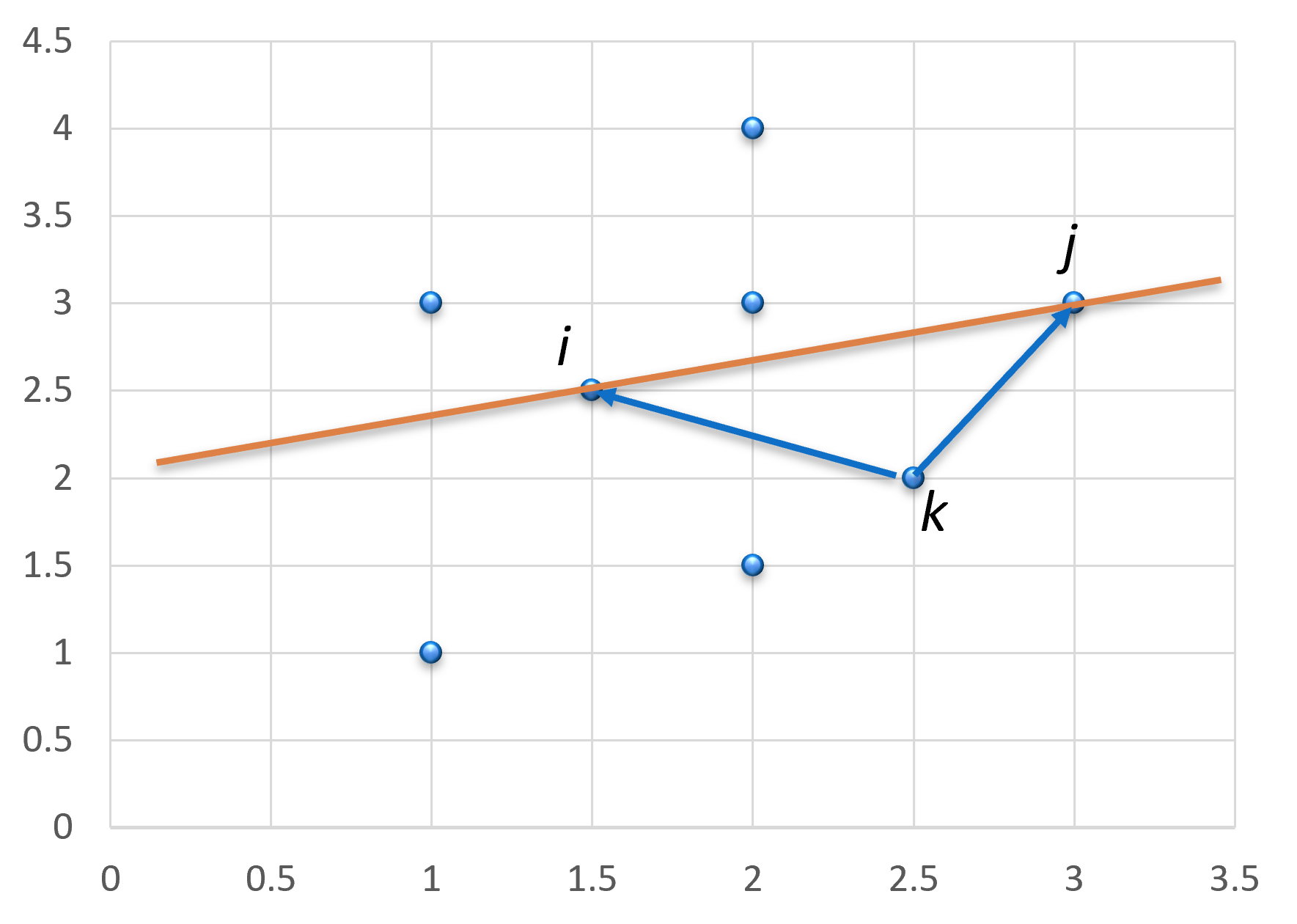
How to check if a point is on the left or right of a line defined by two points?

The following method will return a positive value if the point is on the left of the line, a negative value if the point is on the right of the line, and zero if the point is on the line.

int crossProduct(Point a, Point b, Point c){
    return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
}

Explanation: The cross product of two vectors a and b is defined as the determinant of the matrix formed by the coordinates of the two vectors. The cross product of two vectors a and b is positive if the angle between a and b is less than 180 degrees, negative if the angle is greater than 180 degrees, and zero if the angle is 180 degrees.

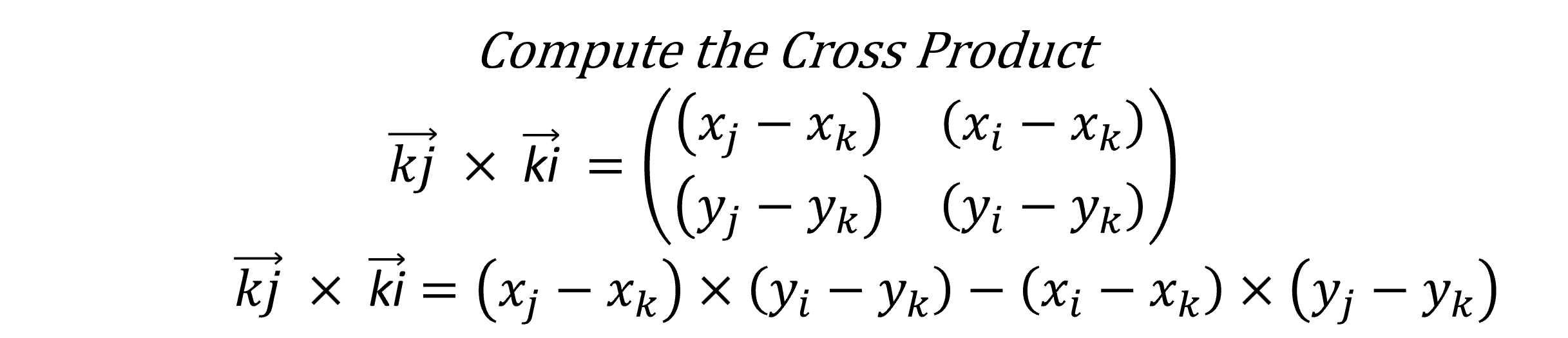
The next step is to implement the brute force algorithm. The brute force algorithm will have a method called convexHull that takes a list of points as input and returns a map that represents the convex hull. The map will have the points of the convex hull as keys and the next point in the convex hull as values.

Map<Point, Point> convexHull(Point[] points) {
    int n = points.length;
    Map<Point, Point> result = new HashMap<>();
    // If the number of points is less than or equal to 3, return the 3 points as the convex hull
    if (n <= 3){
        for(int i = 0; i < n; i++){
            result.put(points[i], points[(i+1)%n]);
        }
        return result;
    }
    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) {
            Point p = points[i];
            Point q = points[j];
            /****************************************
            Check if all other points are on the same semiplane 
            defined by the line (p, q) => all other points have the same 
            sign (positive or negative) of the cross product
            ****************************************/
            int sign = 0; 
            for (int k = 0; k < n; k++) {
                if (k == i || k == j)
                    continue;
                Point r = points[k];
                int crossProduct = crossProduct(p, q, r);
                if (sign == 0) {
                    sign = crossProduct > 0 ? 1 : -1;
                } else if (crossProduct * sign < 0) {
                    sign = 0;
                    break;
                }
            }
            if (sign != 0) {
                if(!result.containsKey(p))
                    result.put(p, q);
                else
                    result.put(q, p);
            }
        }
    }
    return result;
}

The full code with a graphical representation of the convex hull and a randomly generated set of points can be found here.

• 2024 2
• 2023 1
• 2022 2